弹性椭圆壳体的流固耦合模拟常用于检验浸没边界法的收敛性, 是一个相对简单的基准测试. 通过施加不同的材料模型和初始条件, 可以构造出多种算例, 其中一个静态算例具有解析解, 据我所知, 这是唯一具备解析解的流固耦合基准测试.

几何描述

弹性椭圆壳体的厚度不为零, 其初始构型用参数坐标描述：

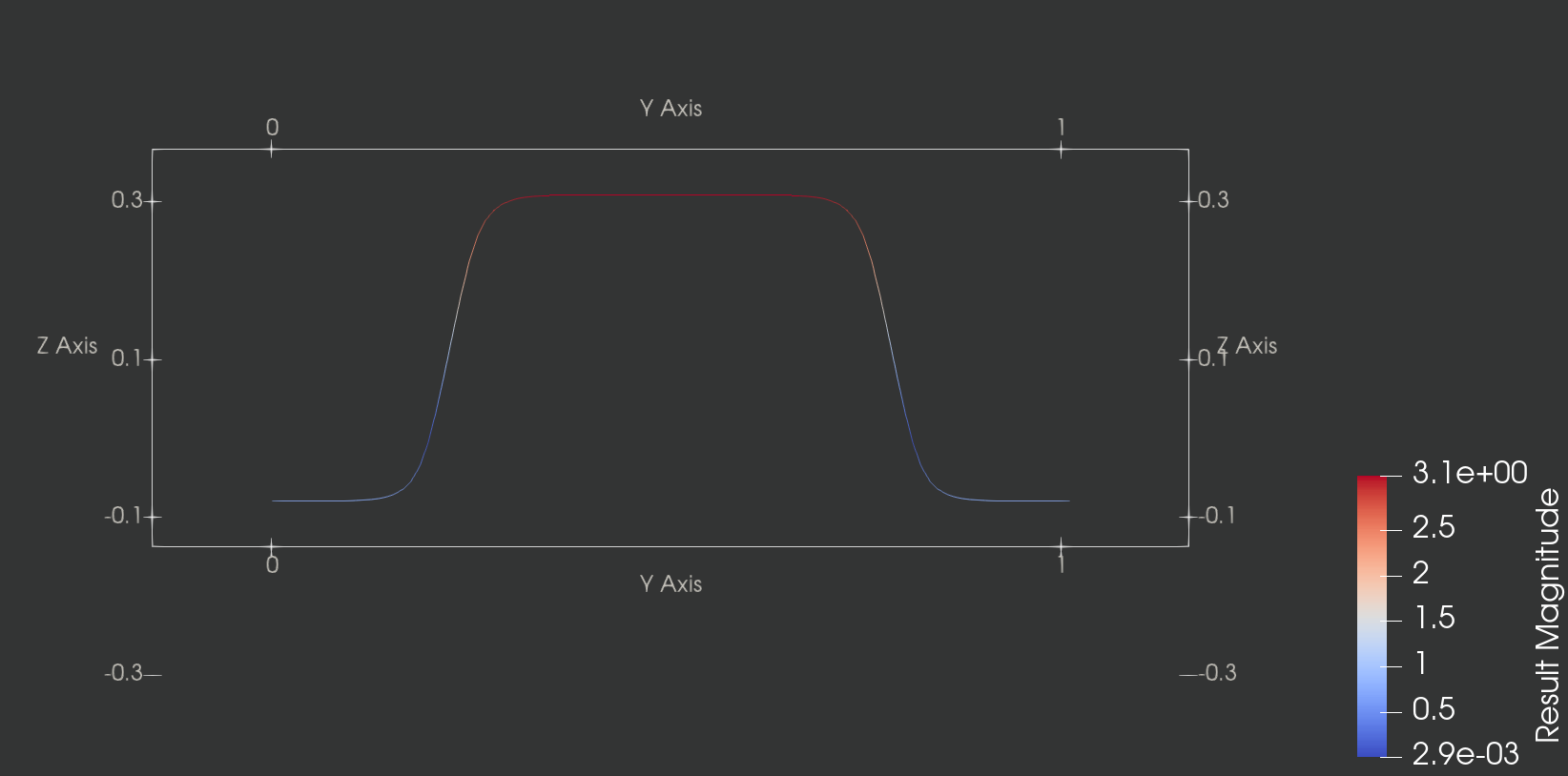
其中, $\textbf{s}=(s_{1},s_{2})\in U=[0,2\pi R]\times[0,\omega]$, 区域 $U$ 在 $s_1$ 方向上是周期性的. 当$\gamma=0$时, 壳体为半径为$R$和厚度为$\omega$的圆环, 处于受力平衡状态, 不会发生变形. 当$\gamma\neq 0$时, 壳体是一个椭圆形环, 处于非平衡状态, 会发生形变，带动流体产生震荡. 为了和参考文献比较, 取$R=0.25$和$\omega=0.0625$, 静态问题使用$\gamma=0$, 动态问题使用$\gamma=0.15$. 流固耦合系统的计算区域为 $\Omega=[0,1]\times[0,1]$ , 周期边界条件¹.

正交异性材料²

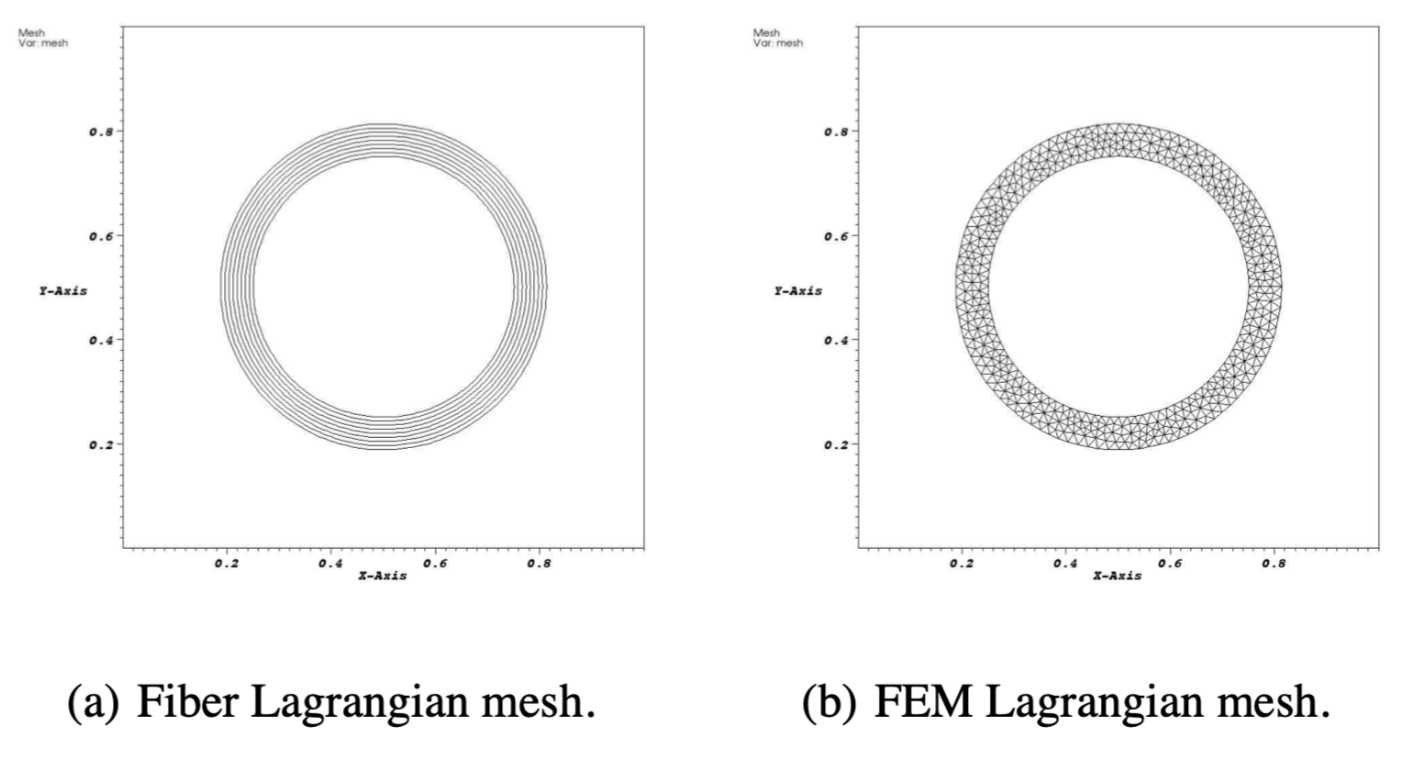
如图 1a所示, 弹性椭圆壳体由沿着圆周方向的纤维构成, 应变能函数为

由于固体的参考构型在 $s_1$ 方向上具有周期性, 在固体边界上始终有$\mathbb{P}^{\mathrm{e}} \mathbf{N} \equiv 0$^{3 4}.

固体力的计算

固体力在参考构型中的计算, 即以 $\mathbf{s}$ 为自变量. 第一PK应力张量为

内力密度 $\mathbf{G}$ 为 ⁵

当$\gamma=0$时, 弹性椭圆壳体处于静止状态, $p$的解析解为

其中, $r=|\mathbf{x}-(0.5,0.5)|$, $p_0$ 的选取可以使 $\int_\Omega p,\mathrm{d}\mathbf{x}=0$, $p$ 的具体推到可参考可参考 heltai 的文章⁶, Boffi 的文章⁷是错的. $\mathbf{u}=\mathbf{0}$.

neo-Hookean 模型

Neo-Hookean 材料

有两种情况:

1. 由沿着圆周方向和沿着径向的纤维构成.
2. 不再考虑纤维，以初始构型为参考坐标.

其中沿着径向的纤维在边界处中断, 这导致压强和粘性力在界面处是间断的, 这也导致了 partitioned formulation 和 unified formulation 的计算结果不同. 大部分情况下, 两种方法计算出来的位移精度差不多, 但是当固体网格较粗时, partitioned formulation 算出压强的结果好一点, 能更好地维持体积守恒性.

应变能函数为

其中$\mathbb{C}=\mathbb{F}^{T}\mathbb{F}$, $I_{1}(\mathbb{C})=tr(\mathbb{F})$,

当$\gamma=0$时, 结构体处于平衡状态, 施加条件$\int_{\Omega}p(x,t)dx=0$, 可得 $$ p(x,t)=

\begin{cases} p_{0}+\mu^{s}(\frac{1}{R}-\frac{1}{R+w}), &r\leq R,\ p_{0}+\frac{\mu^{s}}{w}(\frac{1}{R}(R+w+r)+\frac{R}{R+w}) &R<r\leq R+w\ p_{0}&R+w<r. \end{cases} $$ 其中$r=||x-(0.5,0.5)||$和$p_{0}=\frac{\pi\mu^{e}}{3w}(3wR+R^{2}-\frac{(R+w)^{3}}{R})$.

画出收敛率折线图

1. 总共有五条线, 三条为计算结果, 两条斜率为1和2的参考线.
2. 三条计算结果分别为Mac=1, 2, 4的线.
3. 每条线上的节点分别对应背景网格64, 128, 256, 512, 1024五个数据.
4. 时间步长为0.24*dx.
5. 速度分别依L1, L2, L∞ 范数2阶收敛.
6. 压强分别依L1, L2, L∞ 范数2阶、1.5阶、1阶收敛.
7. 令$\rho=1,\mu=1,$和$\mu^{e}=1$

在测试中, 计算区域$\Omega$离散为$N\times N$的笛卡尔网格, $\Delta x$ 为网格间距. 固体区域$U$离散为$28M\times M$的四边形网格, $M=\frac{1}{M_{fac}}\frac{N}{16}$, 网格间距约为$M_{fa c}\Delta x$, 有限元空间使用了$Q{1}$元⁸.

此外, 由于某些 $\mathbb{P}$ 的选择允许IB方法达到更高阶的收敛率, 这个基准问题可以验证我们的算法能否达到数值格式的精度.

令$\rho=1,\mu=1,$和$\mu^{e}=1$,我们考虑时间区间$0\leq t\leq 3$.图8总结了在时间$t=3$时, 使用$M_{fac}=1,2,4$且$\Delta t=0.25\Delta x$,$N=64,128,256,512$和$1024$的误差数据.$u$的所有范数都可以观察到一阶收敛性. 一阶收敛性也可以通过$p$的$L^{1}$范数观到. $p$在此问题的流固耦合界面上是不连续的. 然而当前的方法在$L^{2}$范数下产生的收敛速率是0.5和在$L^{\infty}$范数下是不收敛的.

我们还考虑了$\gamma=0.15$,使得壳在初始坐标下是不平衡的. 我们设$\mu=0.01$,$\rho=1$,且$\mu^{e}=1$,产生了大约为100的雷诺数. 我们考虑的时间区间大约是$0\leq t\leq 1.25$,其关于壳大约是一个阻尼振动. 同样没有一个精确解, 因此收敛率使用Richardson 插值估计. 图9 总结了当$N=64,128,256,$和$512$且$M_{fac}=1$和$4$且$\Delta t =0.25\Delta x,$$t=0.75s$的误差数据. 对于$u$和$\chi$的所有范数都可以观察到一节收敛率, 然而$p$只在$L^{1}$范数下可观察到一阶收敛率.

对于这个问题我们观察到统一的和分离的公式对于$u$和$\chi$产生相似的精确解.