Turek-Hron 基准算例

本文参考了 Lee J H ¹。该测试最初由 Turek 和 Hron 提出，用于对流固耦合算法进行基准测试。

该结构由圆心在(0.2m,0.2m), 半径为r=0.05m的静止圆盘

和长0.35m,厚为0.02m的弹性尾巴，示意图如下：

结构周围的矩形区域高$H=0.41m,$ 长$L=6H=2.46m$,即$\Omega=[0.0m,2.46m]\times[0.0m,0.41m].$

速度施加如上所示：

其中$\bar{u}$是平均速度，出口处($x=L$)施加零法向牵引力和零切向速度,$y=0.0m$和$y=0.41m$施加零速度条件。

注意，给定区域的大小和圆盘的中心位置，和原始研究一样，浸没的物体在$y$ 方向上是不对称的。

圆盘用一种近乎刚性的材料来描述，尾部的左端是固定的且固定在圆柱上

本文考虑了两种不同密度比，剪切模数和平均入口速度情况。下表总结了流体和固体的物理性质的相关参数集。

这个算例中我们考虑了泊松比$\nu=0.499$.时间步长为$\Delta t=(0.05s\cdot m^{-1})$, 力的惩罚项参数为$\kappa=(2\times10^{-2}kg\cdot m^{-2})/\Delta t^{2}$和$\eta=(4\times10^{-2}kg\cdot m^{-2})/\Delta t$和对于情形1$N_{cycle}=4$，情形2$N_{cycle}=8$。斯特劳哈尔数为$St=fD/\bar{u}$, 其中$f$是点$A$ 的$y$位移的振荡频率，$D$是圆盘的直径。

下图显示了在密度比$\rho_{0}^{s}/\rho^{f}=10$和雷诺数$Re=100$时，梁与周围流体相互作用时的动力学及其变形。

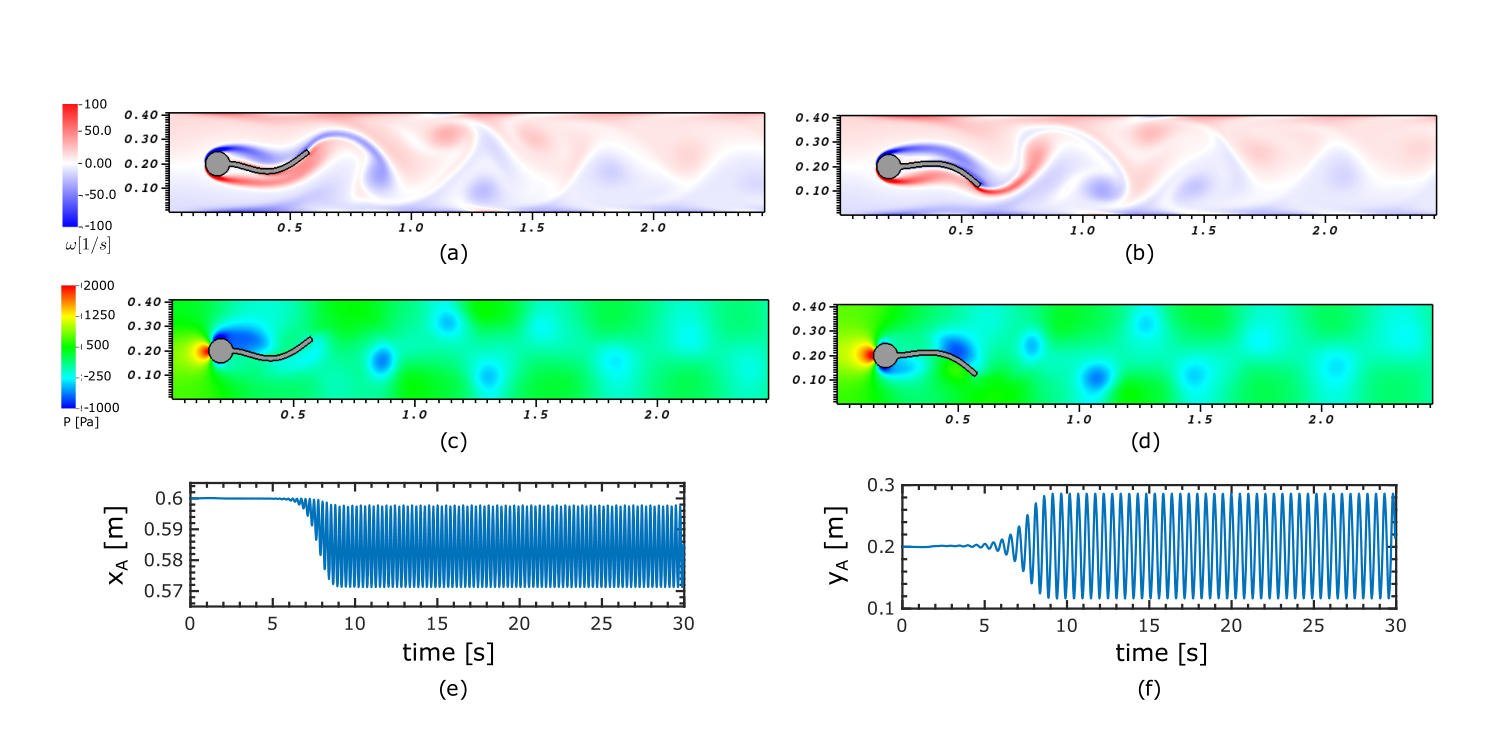
作为额外的验证测试，我们探索了我们的结果在泊松比接近$\nu->5$的极限范围内的敏感性。类似于SEC中的软盘例子。

本构定律：

本文中，我们使用超弹性结构模型，其中第一PK应力张量$P^{s}$与应变能函数有关，对于精确的不可压缩的情形，我们使用了一个几乎不可压缩的结构公式作为惩罚项。对于几乎不可压缩的大变形弹性，我们通过在方程中重新表示$P^{s}$通过$P^{s}=\frac{\partial \psi}{\partial F}$来释放不可压缩约束, 并假定与体积变化和体积保持运动有关的弹性能量的相加分离。这种分离的动机是假设均匀的压力应该产生大小的变化而不是形状的变化，我们首先写出各向同性材料的$\psi$作为标量变量函数，即$\psi=\psi(I_{1},I_{2},I_{3})$.为了获得所需的满足材料框架不变性的分离，我们使用基于Flory分解的标准方法，通过将$F$乘法分解成伸缩部分和偏差部分，$F=J^{1/3}\bar{F}.$这也导致了修正的右柯西—格林应变张量，$\bar{C}=J^{-2/3}C$. 相似地，关于$\bar{C}$的第一个修改不变量是$\bar{I}{1}=J^{-2/3}I{1}$.这个工作中使用的具体模型是$\psi=W(\bar{I_{1}})+U(J)$, 其中$W(\bar{I_{1}})=\bar{W}=W(\bar{F})$用第一个修正不变量来表征材料对剪切变形的反应，$U(J)$是惩罚压缩或膨胀的体积能量，优先选择$U(1)=U^{\prime}(1)=0$.除非另有说明，否则我们使用的neo-Hookean材料模型作为弹性结构

对形变梯度张量$F$可得：

其中$P^{s}{dev}=\frac{\partial W}{\partial \bar{I}{1}}\frac{\bar{I}{1}}{\partial F}$和$P^{s}{dil}=\frac{\partial U}{\partial J}\frac{\partial J}{\partial F}$分别是偏应力（剪应力）和膨胀应力（容积应力). 所以应力分别是

其中$G^{s}$和$K^{s}$是剪切力和体积力，其通过泊松比与$K_{s}=\frac{2G^{s}(1+\nu)}{3(1-2\nu)}$相关.

上述应力公式可以很容易推广到其他各向同性和各向异性本构方程，事实上，目前的ILE公式并不局限于neo-Hookean材料，而且可以很容易使用替代的超弹性甚至非弹性材料模型。

结果对比(WIP)

涡度

旋度和涡度在流体力学中都描述了流场的旋转特性，但它们有具体的区别：

• 旋度 (Vorticity)：指的是速度场的旋转性，数学上定义为速度场 \( \mathbf{u} \) 的旋度，表示为 \( \nabla \times \mathbf{u} \)。旋度是一个矢量量，它的方向表示旋转轴的方向，大小表示旋转强度。
  

  \[ \mathbf{\omega} = \nabla \times \mathbf{u} \]

• 涡度 (Vorticity Magnitude)：通常是旋度的大小，即旋度矢量的模，表示流体旋转的强度，但不包含方向信息。涡度是一个标量量，描述了流体微团绕轴旋转的速率大小：

  \[ |\mathbf{\omega}| = \sqrt{\omega_x^2 + \omega_y^2 + \omega_z^2} \]

在三维情况下，使用分量表示的话，旋度 \( \mathbf{\omega} = (\omega_x, \omega_y, \omega_z) \) 的各个分量为：

在二维流场（例如 \( \mathbf{u} = (u, v) \) ）中，旋度只有垂直于 \( x \)-\( y \) 平面的分量 \( \omega_z \)的分量非零：

这个分量描述了平面流场中流体微元的旋转趋势，数值上与涡度相等。

参考文献

带尾圆柱绕流问题的参考文献如下^1234567：