Windkessel模型

主要参考：关德宝、王英杰的博士毕业论文。详见:appendix-0001

要看 windkessel 模型更详细的实现过程, 详见:appendix-0002

左心室

开环系统

主要参考关德宝、王英杰的博士毕业论文，构建左心室动态收缩的数值模型。根据高老师的建议，初步采用三元素Windkessel模型与左心室进行耦合建模，形成一个开环系统。

使用主动脉压力近似左心室压力
在舒张期结束时接入Windkessel模型
以左心室容积变化作为模型输入
通过模型反馈获取左心室压力参数

当前遇到的主要技术难点在于压力过渡过程的模拟：

左心室舒张末期的压强为8mmHg，需上升至80mmHg后方可应用现有模型。因此需要采用经验性线性函数描述压力跃升过程，或寻求其他更合理的建模方法。关德宝说这个过程可能会遇到一个问题，如果压强的变化和主动收缩力不匹配，那么会出现左心室扩张过大或者剧烈收缩的现象，导致求解失败。

开环系统

闭环系统

下图修改自德宝论文¹的补充材料。

闭环系统

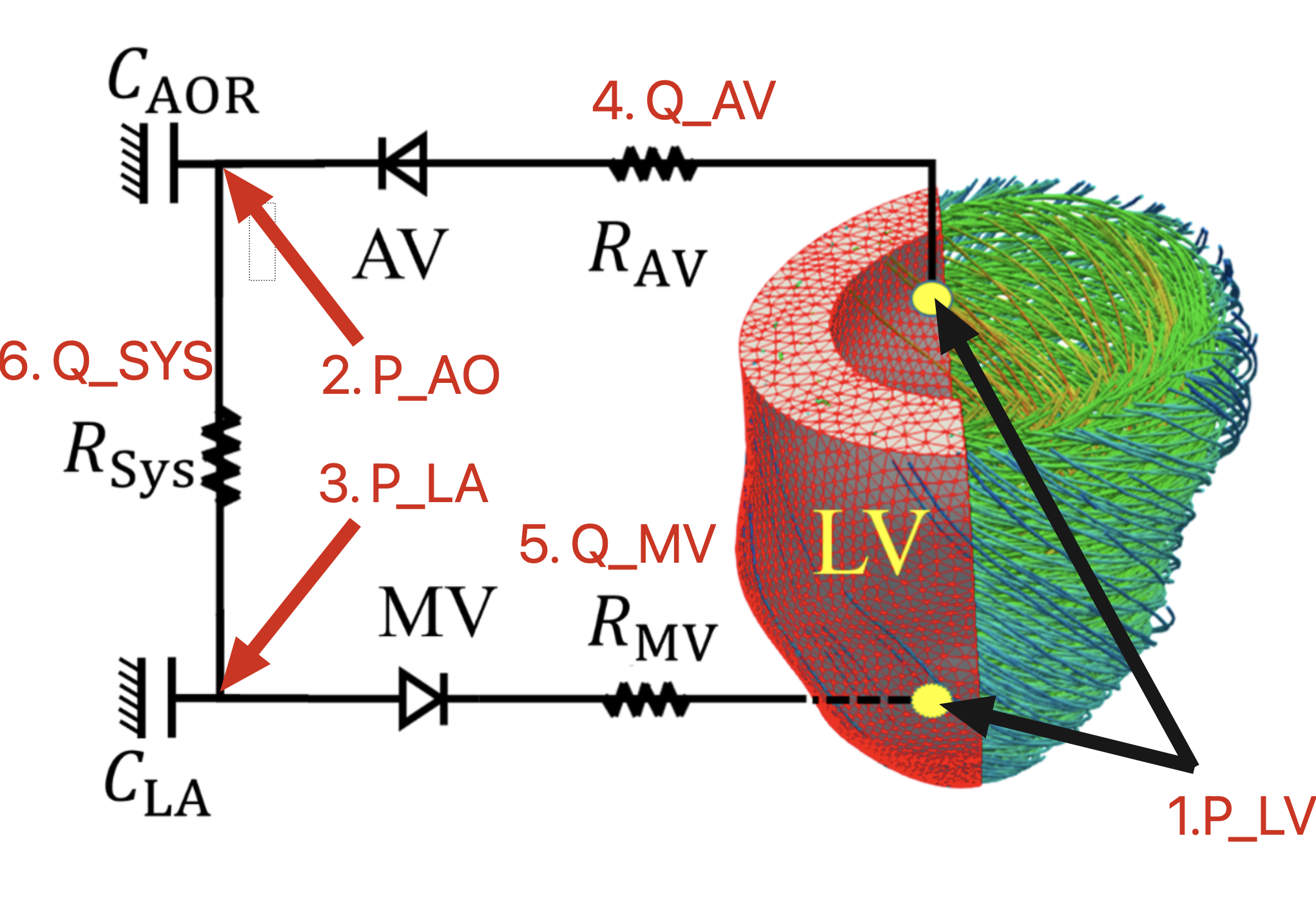
输入物理量：左心室流量 $Q_{LV}$, 输出物理量：左心室压力 $P_{LV}$. 通过Windkessel模型联立六个方程，求解以下六个关键血流动力学物理量：

参数类型	符号表示	物理意义
流量	$Q_{AV}$	主动脉瓣流量
	$Q_{MV}$	二尖瓣流量
	$Q_{SYS}$	体循环流量
压强	$P_{LV}$	左心室压力
	$P_{AO}$	主动脉压力
	$P_{LA}$	左心房压力

六个方程分别为：

主动脉电容方程：

$$ C_{AOR} \frac{dP_{AOR}}{dt} = Q_{AV} - \frac{P_{AOR} - P_{LA}}{R_{SYS}} $$

左心房电容方程：

$$ C_{LA} \frac{dP_{LA}}{dt} = \frac{P_{AOR} - P_{LA}}{R_{SYS}} - Q_{MV} $$

系统流量：

$$ Q_{\text{Sys}}=\frac{P_{\text{AOR}}-P_\text{LA}}{R_\text{Sys}} $$

主动脉瓣（AV）流量：

$$ Q_{AV} = \begin{cases} \frac{P_{LV} - P_{AOR}}{R_{AV}}, & \text{if } P_{LV} > P_{AOR} \ (\text{瓣膜开放}) \\ 0, & \text{otherwise} \end{cases} $$

二尖瓣（MV）流量：

$$ Q_{MV} = \begin{cases} \frac{P_{LA} - P_{LV}}{R_{MV}}, & \text{if } P_{LA} > P_{LV} \ (\text{瓣膜开放}) \\ 0, & \text{otherwise} \end{cases} $$

左心室容积变化方程（通过力学方程反馈）：

$$ \frac{dV_{LV}}{dt} = Q_{MV} - Q_{AV} $$

主要困难

文献中采用的Windkessel等效电路模型参数不能直接移植使用。

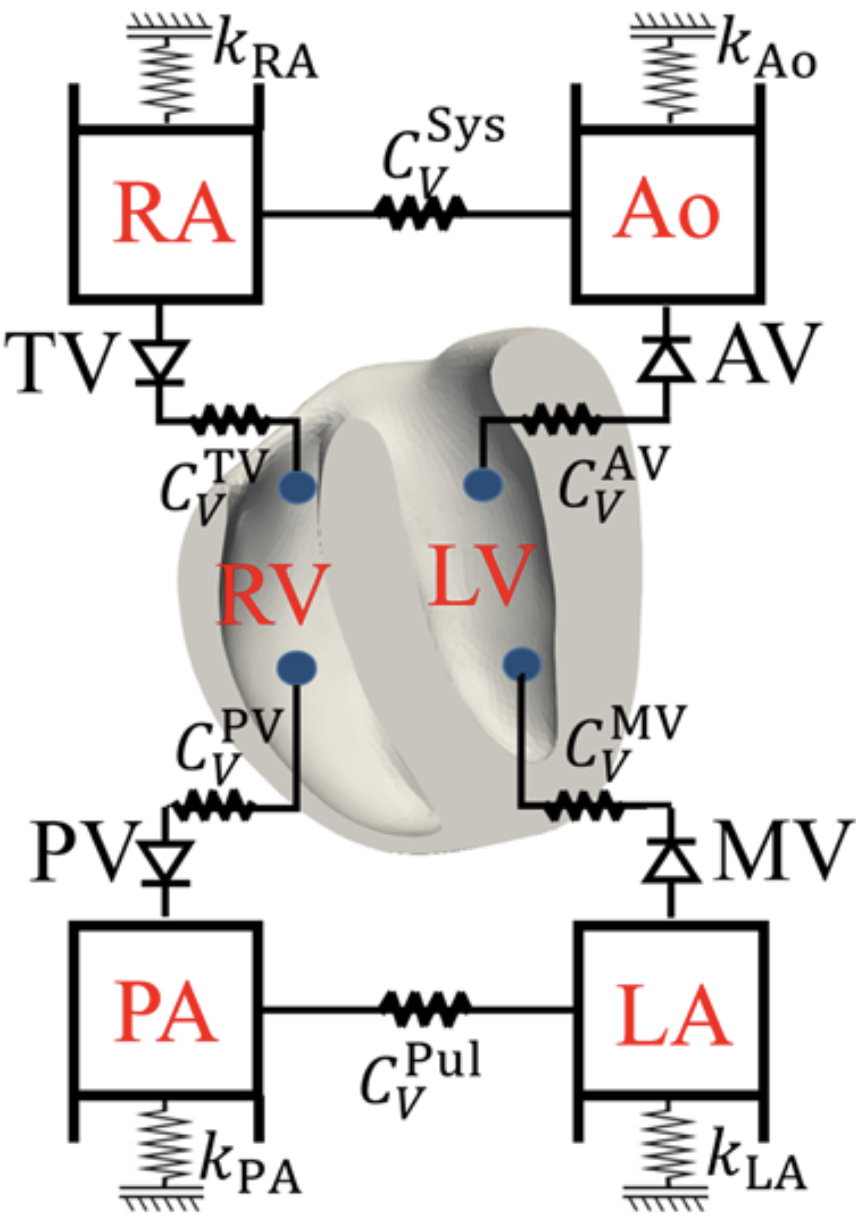
双心室

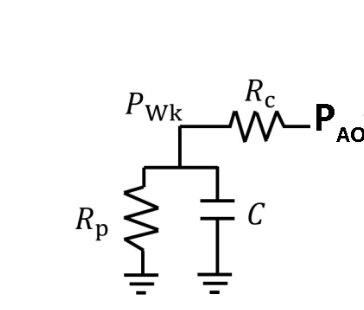
$$ C\frac{dP_\mathrm{WK}}{dt}+\frac{P_\mathrm{WK}}{R_\mathrm{p}}=Q_\mathrm{AO},\\ \frac{P-P_\mathrm{WK}}{R_\mathrm{c}}=Q_\mathrm{AO}. $$ $$ C\frac{P^{n+1}_\mathrm{WK}-P^n_\mathrm{WK}}{\Delta t}+\frac{P^{n+1}_\mathrm{WK}}{R_\mathrm{p}}=Q^{n+1}_\mathrm{AO},\\ \frac{P^{n+1}-P^{n+1}_\mathrm{WK}}{R_\mathrm{c}}=Q^{n+1}_\mathrm{AO}. $$$$ P_{WK}^{n+1}=\left(Q_{AO}^{n+1}+\frac{C}{\Delta t}P^n_{WK}\right)/(\frac{C}{\Delta t}+\frac{1}{R_{p}})\\ P^{n+1}=P^{n+1}_{WK}+Q_{AO}^{n+1}R_{c} $$

高老师，我按您说的，使用三元素的Windkessek模型，采用向后欧拉格式求解，并重新调整了参数，得到如下的左心室内壁压强曲线:

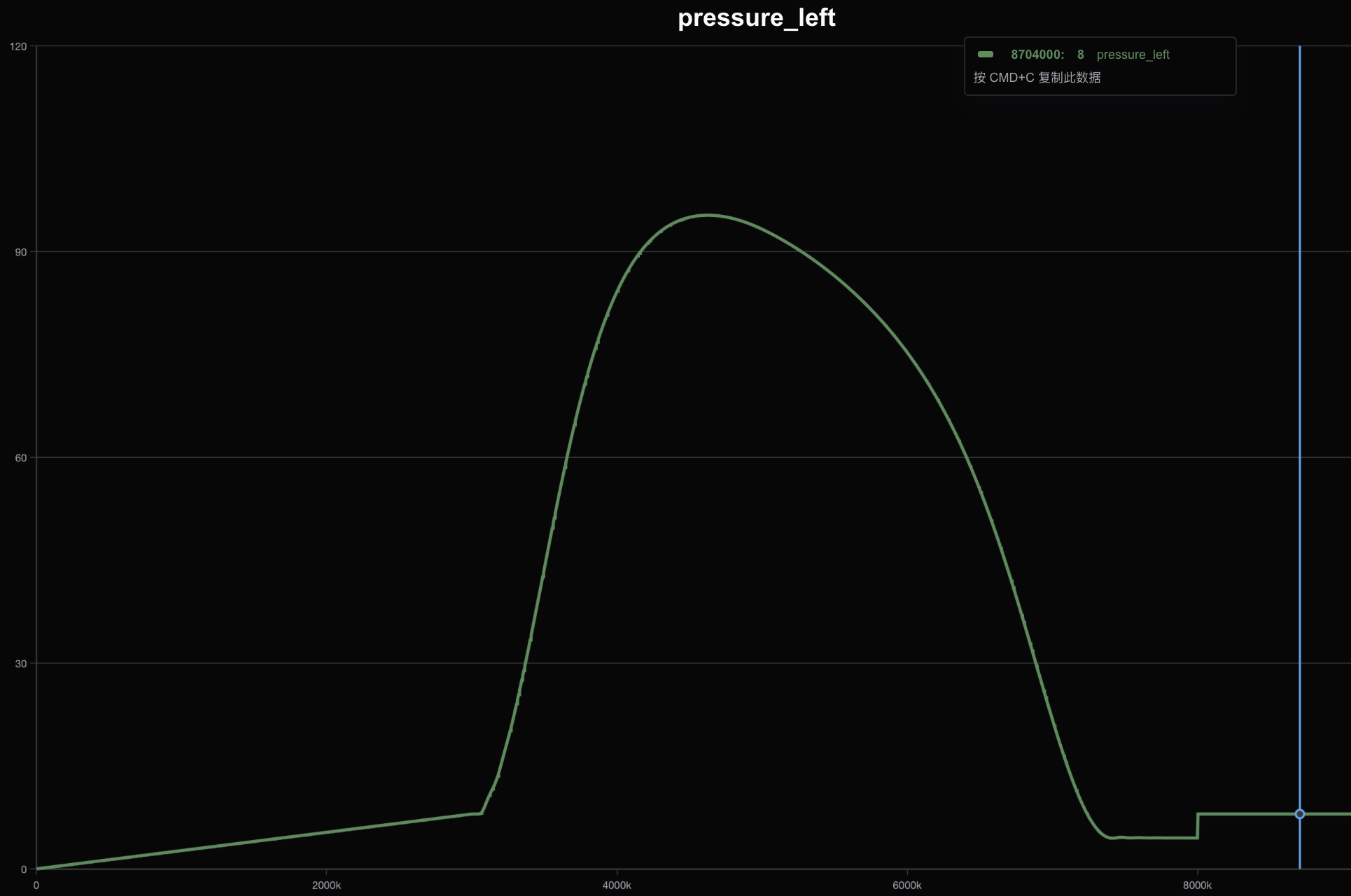
这里，我用 $P_{WK}=P=8\text{mmHg}$ 作为windkessel模型的初值条件(因为舒张末期是8mmHg，不知道怎么升到80mmHg，这个问题还问了德宝)，没有区分主动脉压强和左心室压强，直接把主动脉压强当作左心室压强。

我有个问题，如果我想将主动脉压强施加在冠脉上，怎么分别模拟左心室和主动脉压强？我们尝试求解下面的闭环系统，遇到的困难是不知道怎么处理二极管，比如在舒张末期，左心室压强低于主动脉压强，电路处于断路状态，左心室压强无法更新。

Windkessel 模型对应三种电路图，可通过基尔霍夫定律写出它们的方程。针对二元素windkessel模型，两条定律即可:

干路电流=电容电流+电阻电流
电压=电阻$\times$电流

Open loop

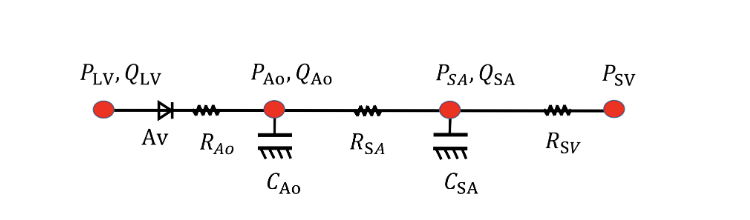
图1为二元素 Windkessel 电路，总共五个参数：$R_{AO}=2.0$, $R_{SA}=120.0$, $R_{SV}=0.8$, $C_{AO}=2.5$, $C_{SA}=1.25$ {cite:p}wang2024modelling 。已知量为静脉端压力$P_{SV}$为($=8 \text{mmHg}$)，从左心室容积随时间变化的函数 $V_{LV}(t)$ 可知$Q_{Ao}$，待求 $P_{LV}$, $P_{AO}$, $P_{SA}$, $Q_{SA}$, $Q_{SV}$五个未知数，可以联立五个方程。

$$ \begin{aligned} Q_{Ao}&=\frac{P_{LV}-P_{AO}}{R_{AO}}\\ Q_{SA}&=\frac{P_{Ao}-P_{SA}}{R_{SA}} \\ Q_{SV}&=\frac{P_{SA}-P_{SV}}{R_{SV}} \\ Q_{SA}&=Q_{AO}-C_{AO}\frac{dP_{AO}}{dt}\\ Q_{SV}&=Q_{SA}-C_{SA}\frac{dP_{SA}}{dt} \end{aligned} $$

三元素Windkessel模型

我们采用一个三元件的Windkessel模型：主动脉流量首先通过一个电阻 $R_c$ 与左心室连接，对应的压强关系为 $P_{ao} - P_{wk} = Q_{ao} \cdot R_c$。接着，流体通过一个串联电阻 $R_p$，该电阻与一个电容 $C$ 并联，模拟血管的顺应性。在舒张期（diastole），左心室压强与主动脉压强存在明显差异；而在收缩期（systole），两者则基本相等。在舒张期内，我们将左心室压强设置为恒定的 8 mmHg；在收缩期，则通过Windkessel模型动态反馈左心室压强。在第一个心动周期的前 0.5 秒内，左心室压强线性上升，模拟前负荷加载过程，最终在舒张末期达到 8 mmHg，随后进入等容收缩期，此时整个左心室同时开始收缩。约在 $t \approx 0.6$ 秒时，左心室腔压超过主动脉压（约 80 mmHg），开始射血期；当左心室压强再次低于主动脉压时，射血结束。在Windkessel模型中引入一个二极管（或理想单向阀） 是很常见的做法，尤其在数值模拟中用以阻止舒张早期的反向流动。这个元件可以在模型中模拟主动脉瓣的单向流动特性，使得当左心室压强低于主动脉压时，血液不会倒流回心室。

求解常微分方程组(TODO)

给定Qao=Qlv, Pao,关于时间的变化，以及参数$Cao=2.5, Csa=1.25, Rao=2.0, Rsa=120$，求解下面的常微分方程组，绘制P_LV的曲线

$$ \begin{aligned} -\frac{P_{LV}^{n+1}}{R_{AO}}&=-Q_{LV}^{n+1}-\frac{P_{AO}^{n+1}}{R_{AO}}\\ Q_{SV}^{n+1}-\frac{P_{SA}^{n+1}}{R_{SV}}&=-\frac{P_{SV}^{n+1}}{R_{SV}}\\ Q_{SA}^{n+1}&=Q_{AO}^{n+1}-C_{AO}\frac{P_{AO}^{n+1}-P_{AO}^{n}}{\Delta t}\\ Q_{SV}^{n+1}-Q_{SA}^{n+1}+C_{SA}\frac{P_{SA}^{n+1}}{\Delta t}&=C_{SA}\frac{P_{SA}^{n}}{\Delta t} \end{aligned} $$$$ \begin{pmatrix} -\frac{1}{R_{AO}} & 0 & 0 & 0 \\ 0 & -\frac{1}{R_{SV}} & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & \frac{C_{SA}}{\Delta t} & 1 & -1 \\ \end{pmatrix} \begin{pmatrix} P_{LV}^{n+1} \\ P_{SA}^{n+1} \\ Q_{SV}^{n+1} \\ Q_{SA}^{n+1} \end{pmatrix} $$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import numpy as np

def build_coefficient_matrix(Cao, Csa, Rao, Rsa, dt):
    """
    返回给定参数下的 4x4 系数矩阵 A，
    形式为 A @ [P_LV, P_SA, Q_SV, Q_SA]^T
    """
    A = np.array([
        [-1 / Rao,        0,               0,            0],
        [     0,   -1 / Rsa,               1,            0],
        [     0,        0,                 0,            1],
        [     0,   Csa / dt,               1,           -1],
    ])
    return A

def build_rhs_vector(Qlv, Pao, Psv, Qao, Pao_1, Psa, Rao, Rsv, Cao, Csa, dt):
    """
    返回右端向量 b：
    [
        -Qlv - Pao / Rao,
        -Psv / Rsv,
        Qao - Cao/dt * (Pao_1 - Pao),
        Csa/dt * Psa
    ]
    """
    b1 = -Qlv - Pao / Rao
    b2 = -Psv / Rsv
    b3 = Qao - Cao * (Pao_1 - Pao) / dt
    b4 = Csa / dt * Psa

    return np.array([b1, b2, b3, b4])

Modelling of fibre dispersion and its effects on cardiac mechanics from diastole to systole ↩︎