SAV 方法求解 N-S 方程(二)
SAV
半离散格式的构造
这种格式的显著特征是引入了一个与N-S系统总能量关联的辅助变量(auxiliary variable)。辅助变量的定义如下，在定义能量的时候包含了对流项的边界积分。 \[ R(t)=\sqrt{E(t)} \] (3)和(4)为动量方程和辅助变量方程， \[ \frac{\partial \mathbf{u}}{\partial t}+\mathbf{N}(\mathbf{u})+\nabla p-\nu \nabla^2 \mathbf{u}=\mathbf{f},\tag{3} \]
\[ \begin{aligned} 2 R \frac{d R}{d t}=\frac{d E}{d t}=\int_{\Omega} \frac{\partial \mathbf{u}}{\partial t} \cdot \mathbf{u}=\int_{\Omega}\left(\frac{\partial \mathbf{u}}{\partial t}+\mathbf{u} \cdot \nabla \mathbf{u}\right) \cdot \mathbf{u}-\int_{\partial \Omega}(\mathbf{n} \cdot \mathbf{u}) \frac{1}{2}|\mathbf{u}|^2 \end{aligned} \]
根据定义，方程(3)和方程(4)可以修改成(5)和(6)。 \[ \frac{\partial \mathbf{u}}{\partial t}+\frac{R(t)}{\sqrt{E(t)}} \mathbf{N}(\mathbf{u})+\nabla p-v \nabla^2 \mathbf{u}=\mathbf{f} .\tag{5} \] \[ 2 R \frac{d R}{d t}=\int_{\Omega}\left[\frac{\partial \mathbf{u}}{\partial t}+\frac{R(t)}{\sqrt{E(t)}} \mathbf{N}(\mathbf{u})\right] \cdot \mathbf{u}-\int_{\partial \Omega}(\mathbf{n} \cdot \mathbf{u}) \frac{1}{2}|\mathbf{u}|^2 .\tag{6} \]
方程(5)和方程(6)加上以下几个条件后完备。 \[ \begin{aligned} & \mathbf{u}|_{\partial \Omega}=\mathbf{w}(\mathbf{x}, t), \\ & \mathbf{u}(\mathbf{x}, 0)=\mathbf{u}_{i n}(\mathbf{x}), \\ & \int_{\Omega} p=0 , \\ & R(0)=\left(C_0+\int_{\Omega} \frac{1}{2}\left|\mathbf{u}_{i n}\right|^2\right)^{\frac{1}{2}}. \end{aligned} \] 时间离散后，完整的方程组可以写成 \[ \begin{aligned} & \frac{\gamma_0 \mathbf{u}^{n+1}-\hat{\mathbf{u}}}{\Delta t}+\frac{R^{n+1}}{\sqrt{E^{n+1}}} \mathbf{N}\left(\overline{\mathbf{u}}^{n+1}\right)+\nabla p^{n+1}-v \nabla^2 \mathbf{u}^{n+1}=\mathbf{f}^{n+1} \\ & \nabla \cdot \mathbf{u}^{n+1}=0 \\ & 2 R^{n+1} \frac{\gamma_0 R^{n+1}-\hat{R}}{\Delta t}=\int_{\Omega}\left[\frac{\gamma_0 \mathbf{u}^{n+1}-\hat{\mathbf{u}}}{\Delta t}+\frac{R^{n+1}}{\sqrt{E^{n+1}}} \mathbf{N}\left(\overline{\mathbf{u}}^{n+1}\right)\right] \cdot \mathbf{u}^{n+1}-\int_{\partial \Omega}\left(\mathbf{n} \cdot \mathbf{u}^{n+1}\right) \frac{1}{2}\left|\mathbf{u}^{n+1}\right|^2, \\ & \mathbf{u}^{n+1}=\mathbf{w}^{n+1}, \quad \text { on } \partial \Omega \\ & E^{n+1}=\int_{\Omega} \frac{1}{2}\left|\mathbf{u}^{n+1}\right|^2+C_0 \\ & \int p^{n+1}=0 \end{aligned} \]
求解步骤
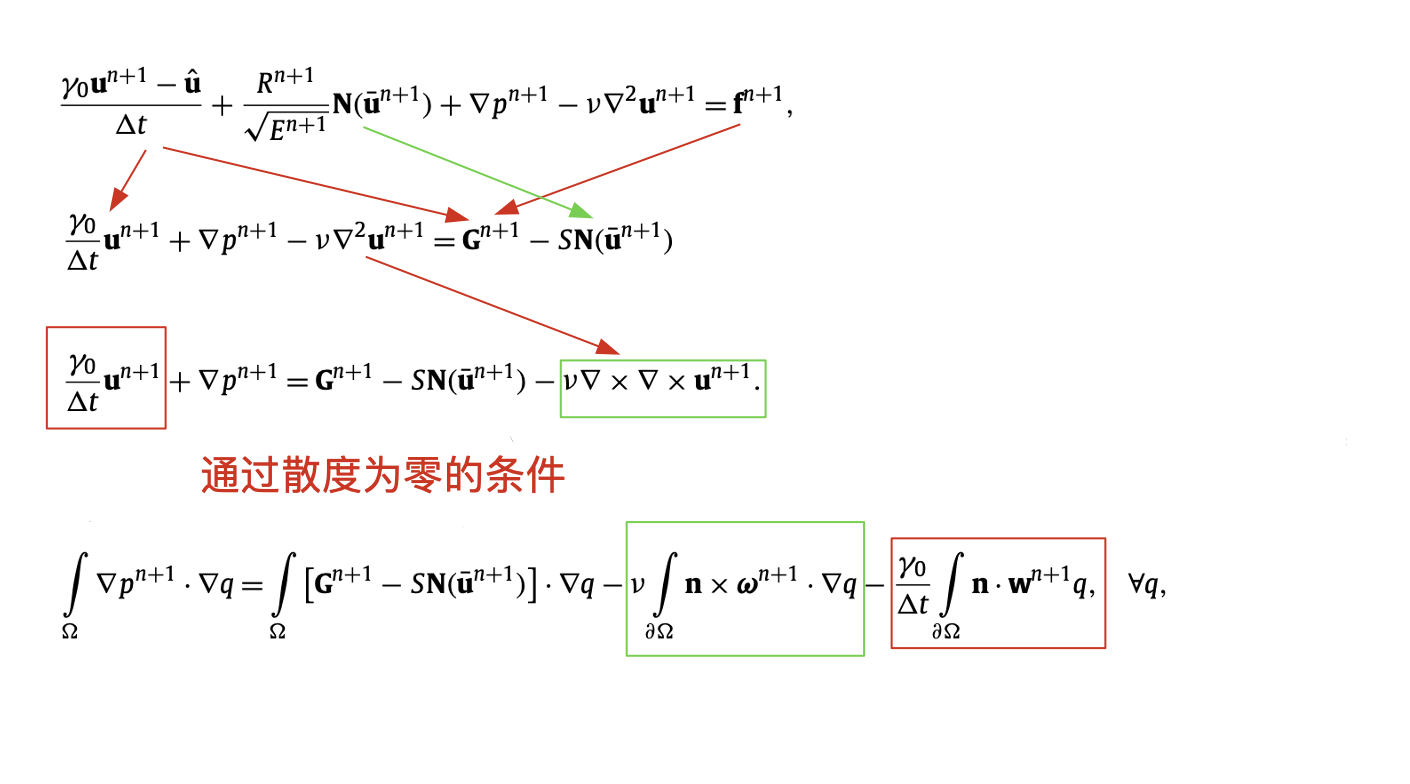
首先从动量方程出发依次推导 \[ \frac{\gamma_0 \mathbf{u}^{n+1}-\hat{\mathbf{u}}}{\Delta t}+\frac{R^{n+1}}{\sqrt{E^{n+1}}} \mathbf{N}\left(\overline{\mathbf{u}}^{n+1}\right)+\nabla p^{n+1}-\nu \nabla^2 \mathbf{u}^{n+1}=\mathbf{f}^{n+1} \]
\[ \frac{\gamma_0}{\Delta t} \mathbf{u}^{n+1}+\nabla p^{n+1}-\nu \nabla^2 \mathbf{u}^{n+1}=\mathbf{G}^{n+1}-S \mathbf{N}\left(\overline{\mathbf{u}}^{n+1}\right)\tag{10} \]
\[ \frac{\gamma_0}{\Delta t} \mathbf{u}^{n+1}+\nabla p^{n+1}=\mathbf{G}^{n+1}-S \mathbf{N}\left(\overline{\mathbf{u}}^{n+1}\right)-\nu \nabla \times \nabla \times \mathbf{u}^{n+1} \]
\[ \int_{\Omega} \nabla p^{n+1} \cdot \nabla q=\int_{\Omega}\left[\mathbf{G}^{n+1}-S \mathbf{N}\left(\overline{\mathbf{u}}^{n+1}\right)\right] \cdot \nabla q-v \int_{\partial \Omega} \mathbf{n} \times \boldsymbol{\omega}^{n+1} \cdot \nabla q-\frac{\gamma_0}{\Delta t} \int_{\partial \Omega} \mathbf{n} \cdot \mathbf{w}^{n+1} q, \quad \forall q,\tag{11} \]
表达式 \(\overline{\boldsymbol{\omega}}^{n+1}=\nabla \times \overline{\mathbf{u}}^{n+1}\) 为采用了显式逼近涡量，这一项涉及边界上的空间导数，无法直接通过Dirichlet边界条件计算出来。这样做会降低数值格式的稳定性，但是显著简化了数值计算的复杂度，降低了大量计算。
求解步骤
求解p1和p2
将\(p^{n+1}=p_1^{n+1}+S p_2^{n+1}\) 代入方程(11)，分离出含有S得项和不含S的项。 \[ \begin{gathered} \int_{\Omega} \nabla p_1^{n+1} \cdot \nabla q=\int_{\Omega} \mathbf{G}^{n+1} \cdot \nabla q-\nu \int_{\partial \Omega} \mathbf{n} \times \overline{\boldsymbol{\omega}}^{n+1} \cdot \nabla q-\frac{\gamma_0}{\Delta t} \int_{\partial \Omega} \mathbf{n} \cdot \mathbf{w}^{n+1} q, \quad \forall q , \end{gathered} \]
\[ \int_{\Omega} \nabla p_2^{n+1} \cdot \nabla q=-\int_{\Omega} \mathbf{N}\left(\overline{\mathbf{u}}^{n+1}\right) \cdot \nabla q, \quad \forall q. \]
求解u1和u2
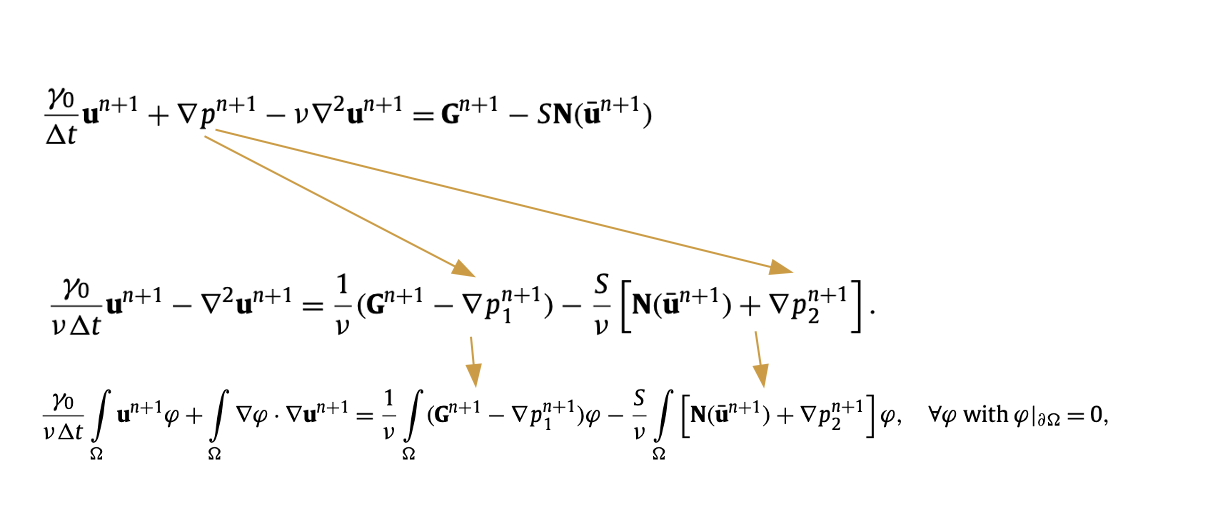首先对方程(10)进行分解，得到方程(15) \[ \frac{\gamma_0}{\nu \Delta t} \int_{\Omega} \mathbf{u}^{n+1} \varphi+\int_{\Omega} \nabla \varphi \cdot \nabla \mathbf{u}^{n+1}=\frac{1}{v} \int_{\Omega}\left(\mathbf{G}^{n+1}-\nabla p_1^{n+1}\right) \varphi-\frac{S}{v} \int_{\Omega}\left[\mathbf{N}\left(\overline{\mathbf{u}}^{n+1}\right)+\nabla p_2^{n+1}\right] \varphi\tag{15} \]
将\(\mathbf{u}^{n+1}=\mathbf{u}_1^{n+1}+S \mathbf{u}_2^{n+1}\)代入方程，再进行同类项的合并，可得到 \[ \frac{\gamma_0}{v \Delta t} \int_{\Omega} \mathbf{u}_1^{n+1} \varphi+\int_{\Omega} \nabla \varphi \cdot \nabla \mathbf{u}_1^{n+1}=\frac{1}{v} \int_{\Omega}\left(\mathbf{G}^{n+1}-\nabla p_1^{n+1}\right) \varphi, \quad \forall \left.\varphi\right|_{\partial \Omega}=0 \text {. } \] \(\mathbf{u}_1^{n+1}=\mathbf{w}^{n+1}, \quad\) \[ \frac{\gamma_0}{v \Delta t} \int_{\Omega} \mathbf{u}_2^{n+1} \varphi+\int_{\Omega} \nabla \varphi \cdot \nabla \mathbf{u}_2^{n+1}=-\frac{1}{\nu} \int_{\Omega}\left[\mathbf{N}\left(\overline{\mathbf{u}}^{n+1}\right)+\nabla p_2^{n+1}\right] \varphi, \quad \forall \varphi|_{\partial \Omega}=0 \] \(\left.\varphi\right|_{\partial \Omega}=0\)
\(\mathbf{u}_2^{n+1}=0, \quad\) on \(\partial \Omega\).
计算辅助变量
\[ F(S)=\frac{2 \gamma_0}{\Delta t} S^3 E(S)-\frac{2 \hat{R}}{\Delta t} S^2 \sqrt{E(S)}+B_0 S+B_1 S^2+B_2 S^3=0 \]