浸没边界法中的限制算子和延拓算子

发表于 2023-06-17 评论数：编辑

限制算子和延拓算子这两个概念的翻译，其实早已存在，例如多重网格方法、区域分解方法，浸没边界法中也有类似的概念。

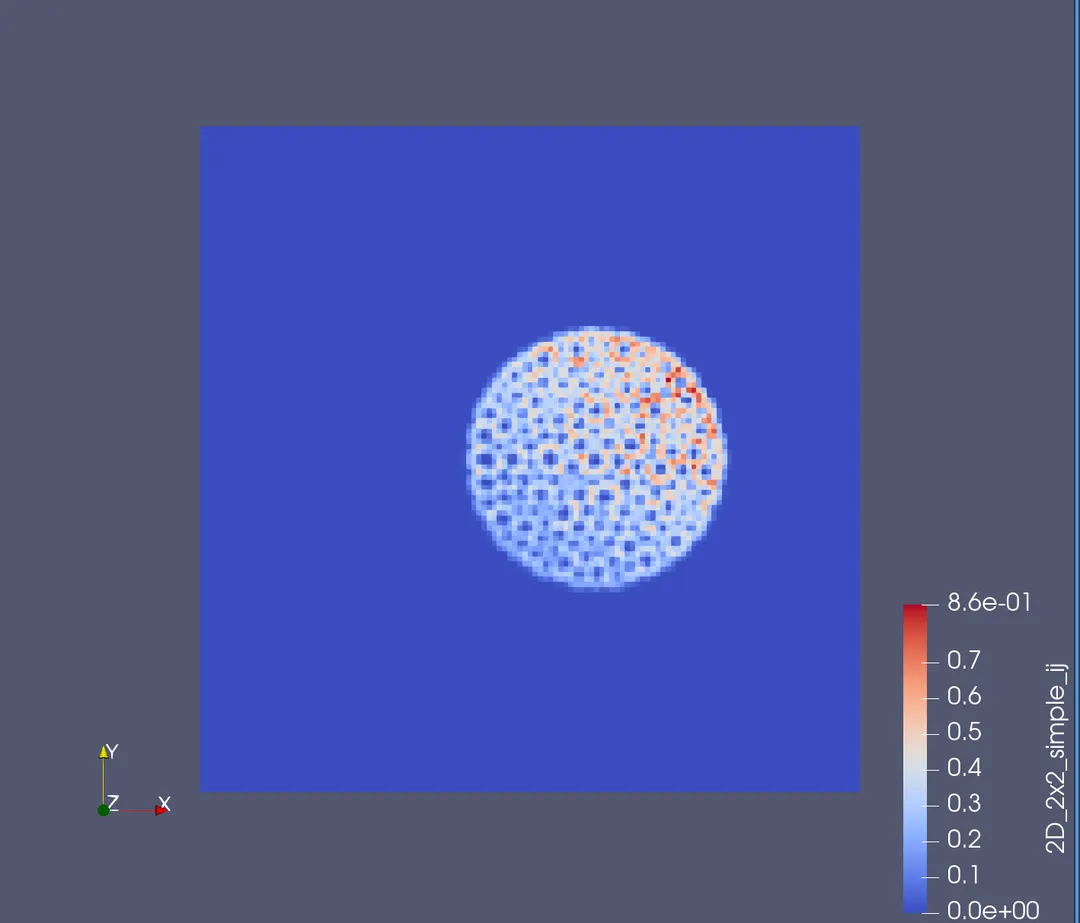
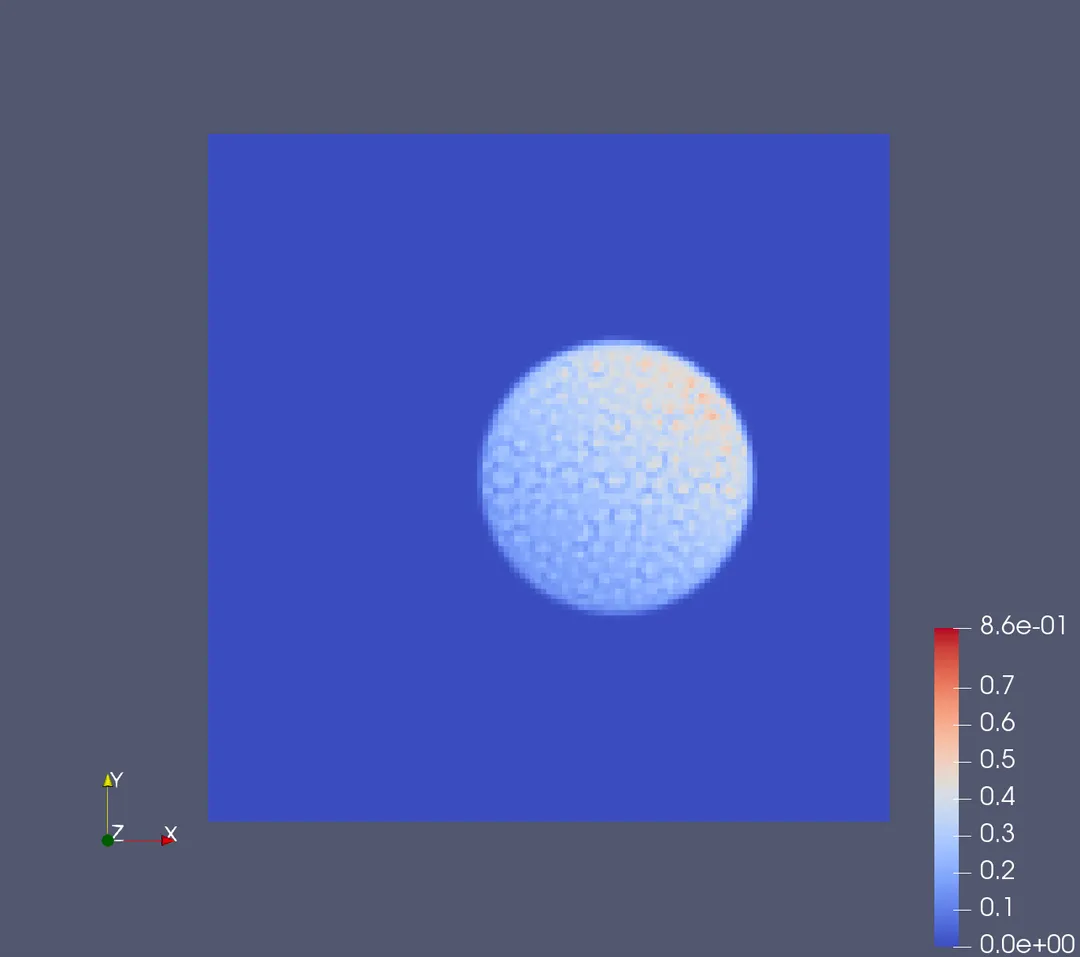
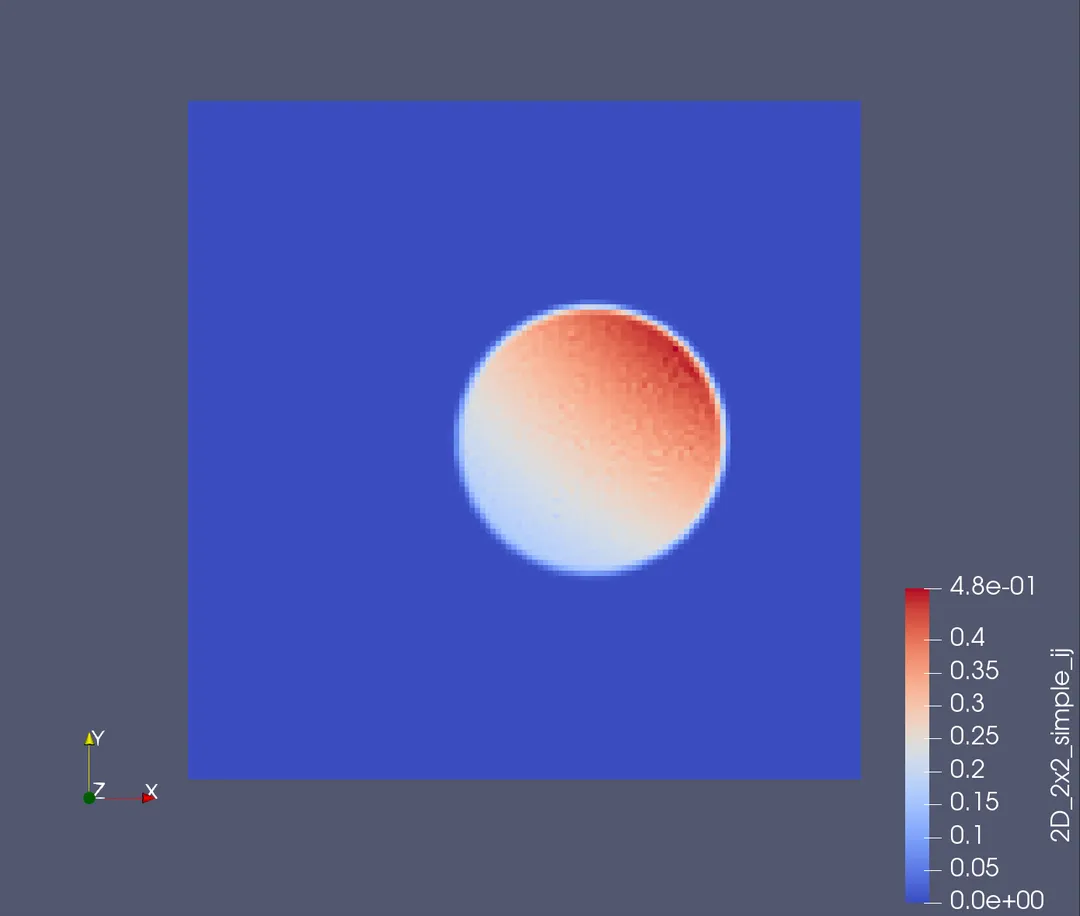
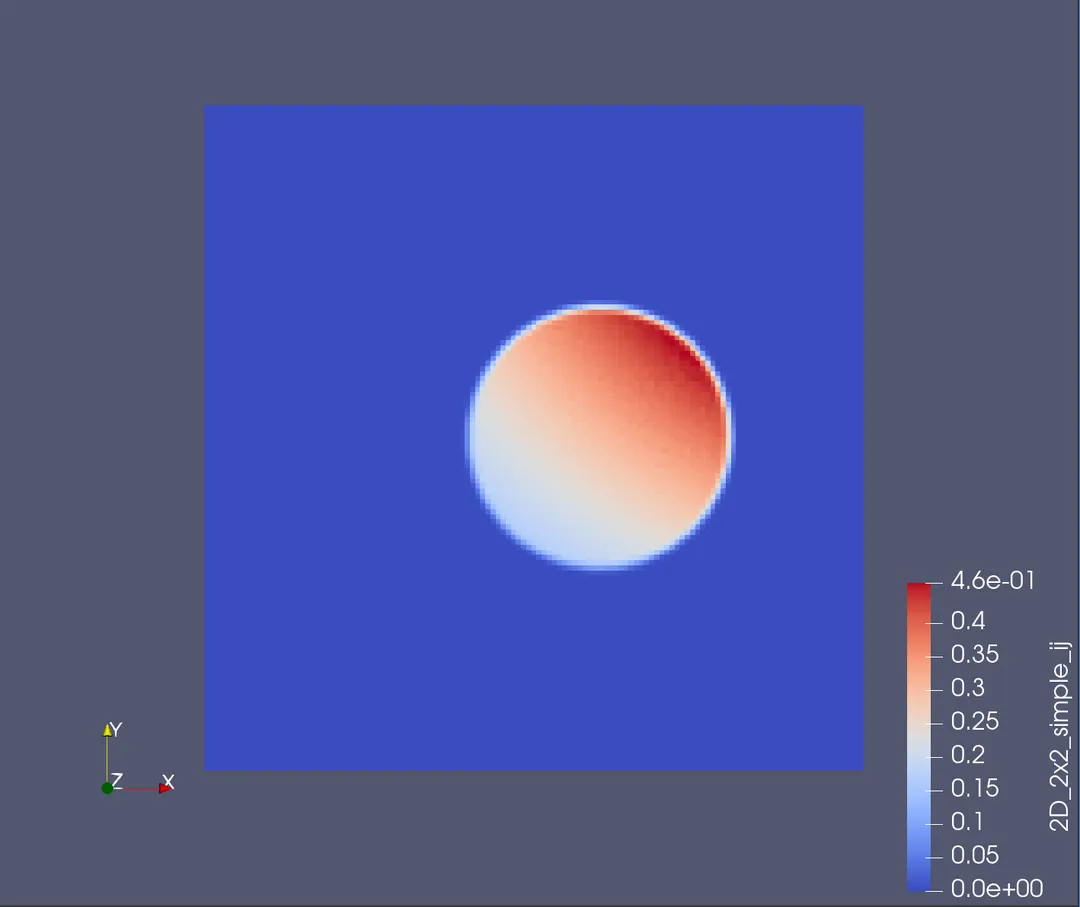
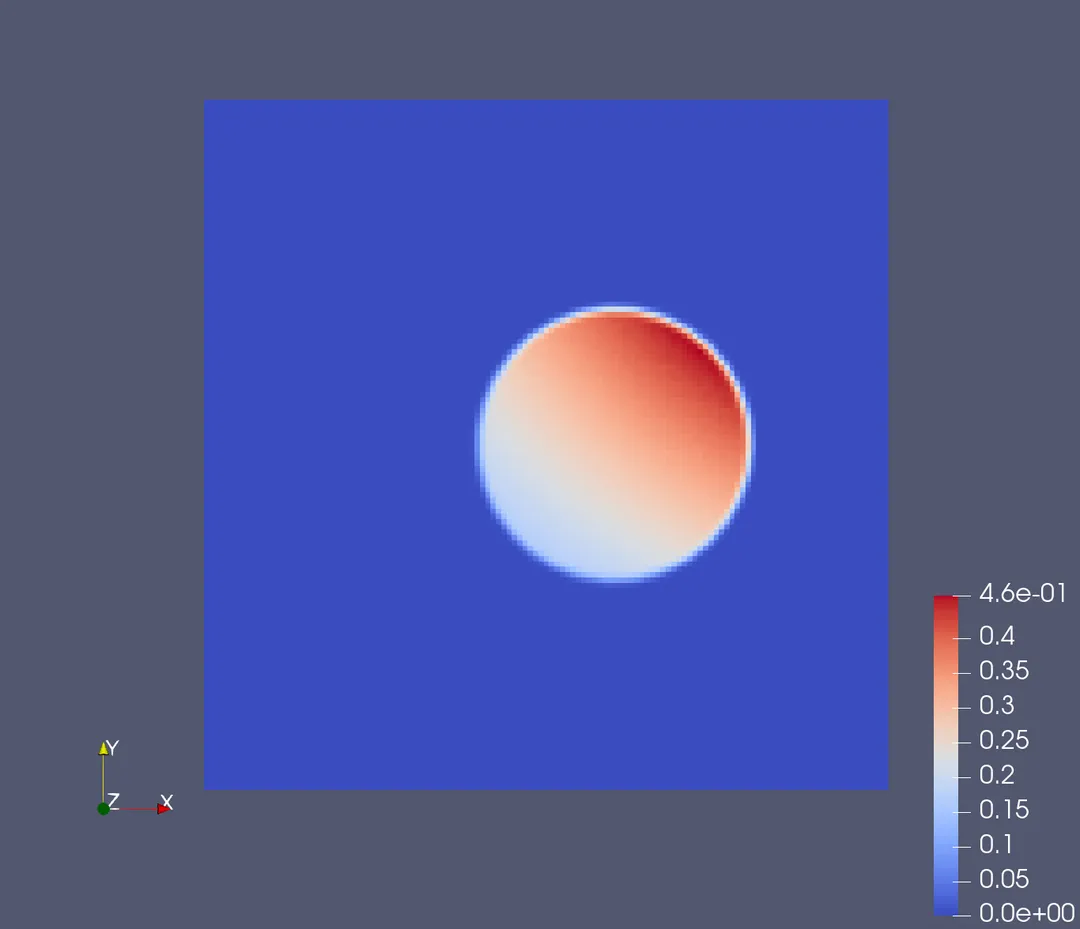
在我们的例子中，固体区域被剖分成398个网格单元，背景区域被剖分成128x128个网格单元。以下分别采用1、3、5、7、9阶高斯积分公式的延拓算子得到的结果。可见，即使固体网格的空间步长远大于背景网格区域，物理量从固体区域延拓到背景区域后仍能较好地维持原来的性质。

采用不同精度的高斯积分法对结果产生的影响

不同类型的数据之间的交互通过两组函数来进行，第一组是split和merge，第二组是flatten和ripple。split将二维或三维空间中的向量分解成独立的分量，例如将

\{\{x_1,y_1,z_1\},\{x_2,y_2,z_2\},...,\{x_N,y_N,z_N\}\}

分解成

\{x_1,x_2,...,x_N\},\;\{y_1,y_2,...y_N\},\;\{z_1,z_2,...,z_N\},

merge则相反。flatten将向量

\{\{x_1,y_1,z_1\},\{x_2,y_2,z_2\},...,\{x_N,y_N,z_N\}\}

推平成

\{x_1,y_1,z_1,x_2,y_2,z_2,...,x_N,y_N,z_N\},

ripple则相反，将平整的数据压皱。

FEniCS求解方腔顶盖流

FEniCS求解方腔顶盖流的算例不知道写了多少回的，每次要用的时候都要重新写重新改。现把程序贴在此处，以便日后之需。此算例输出区域内位于直线 $x=0.5$ ， $u$ 分量的值，一共输出64个值。对应流固耦合程序中快照 2c26d0c78a168f3f470f0e56abebda3887522a85 中 mesh_ibm_2D.cpp 文件的test_lid_driven函数。

from fenics import *

# Set parameter values
nu = 0.01
N = 32
T = 0.01
dt = 0.0001
mesh = RectangleMesh(Point(0, 0), Point(1, 1), N, N)

def liddriven(T, dt):
    # Define function spaces
    P2 = VectorElement("Lagrange", mesh.ufl_cell(), 2)
    P1 = FiniteElement("Lagrange", mesh.ufl_cell(), 1)
    TH = P2 * P1
    W = FunctionSpace(mesh, TH)

    # Define boundaries
    upflow = 'near(x[1], 1.0, DOLFIN_EPS)'
    wall = 'near(x[0], 0.0) || near(x[0], 1.0) || near(x[1], 0.0)'

    # Define boundary conditions
    bcu_inflow = DirichletBC(W.sub(0), Constant((1, 0)), upflow)
    bcu_wall = DirichletBC(W.sub(0), Constant((0, 0)), wall)
    bcu = [bcu_inflow, bcu_wall]

    k = Constant(dt)
    f = Constant((0, 0))
    wn = Function(W)
    (un, _) = wn.split(True)

    # Define variational problem
    (u, p) = TrialFunctions(W)
    (v, q) = TestFunctions(W)
    # F = inner((u-un)/k, v)*dx + inner(grad(un)*un, v)*dx + nu * \
    #     inner(grad(u), grad(v))*dx - div(v)*p * \
    #     dx + q*div(u)*dx - inner(f, v)*dx
    F = inner((u-un)/k, v)*dx + nu * \
        inner(grad(u), grad(v))*dx - div(v)*p * \
        dx + q*div(u)*dx - inner(f, v)*dx
    a = lhs(F)
    L = rhs(F)

    # Assemble matrix and vector
    A = assemble(a)

    t = 0
    w_ = Function(W)
    while t < T - DOLFIN_EPS:
        t += dt
        # Assemble right side term
        b = assemble(L)
        # Compute solution
        [bc.apply(A, b) for bc in bcu]
        solve(A, w_.vector(), b)
        # Update coefficients
        (u_, _) = w_.split(True)
        un.assign(u_)

    for j in range(64):
        un.set_allow_extrapolation(True)
        print(un((0.5, (j+1)/64))[0])


liddriven(T, dt)